概述

本期的重点在于使用8086汇编语言实现循环迭代，无符号数字输出,使用多位内存储存超长整型,超长整型打印输出

程序框图

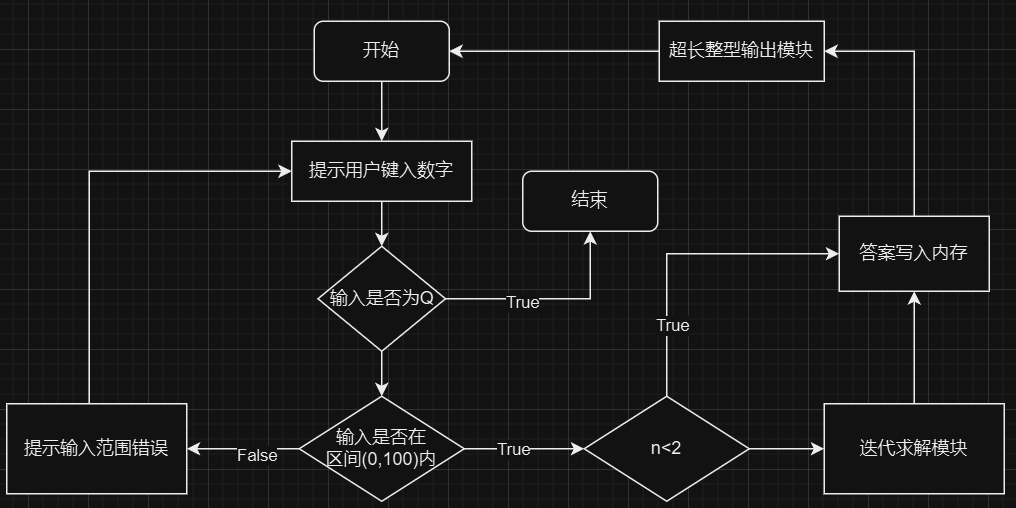
模块图

初始化准备

我们先把代码段、数据段和栈段准备好相关的数据并完成相关的初始化

声明段

我们先声明三个段

1
assume cs:codesg,ds:datasg,ss:stacksg

装载数据

在数据段我们准备填入如下数据

  • choose 字符串,用于输出提示信息
  • result 字符串,用于输出提示信息
  • enter 字符串，用于输出回车换行，即\n\r
  • pressQ 字符串，用于输出退出程序的提示信息
  • wrongRange 字符串，用于输出范围错误的提示信息
  • num1 12字节长整型,表示迭代中的Fib(n-2)
  • num2 12字节长整型，表示迭代中的Fib(n-1),同时最终答案也存在num2中
  • numlen 单字(2字节)变量，储存输出数字串的长度/栈的深度
  • tmpcx1 单字变量，辅助暂存cx的值，避免使用栈，防止栈的管理混乱

这里写入num我们使用dw指令写入一个字长（2字节）

而写入字符串必须一个字节一个字节写入，所以使用db指令

特别的，在8086中，$用于表示一段字符串的结尾

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
;初始化数据段，并填入数字
datasg segment
    choose db 'Please choose a num from 1 to 100 : ','$'
    result db 'The result is : ','$'
    pressQ db 'Presss Q to exit','$'
    wrongRange db 'wrong range, try again'
    enter db 13, 10,'$'
    num1 dw 6 dup(0)
    num2 dw 6 dup(0)

    numlen dw 0 ;储存输出长度

    tmpcx1 dw 0

datasg ends

而对于栈段,其实并不需要做什么特别的初始化，当然我们可以给它额外做个置零

这里对连续内存置零我们使用了dup指令配合db进行重复写入

1
2
3
4
;初始化栈段，置空
stacksg segment
    db 25565 dup(0) ;我们选择栈的大小为25565个字节
stacksg ends

主逻辑框架

最后我们再在代码段把整个程序的主逻辑框架，这里我们会调用一些自定义的模块，但这里只是保留它们的名字和逻辑功能，具体实现交给文章的后半部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
codesg segment
start:  
    mov ax,datasg 
    mov ds,ax;
    mov ax,stacksg;
    mov ss,ax;
    mov sp,25565;初始化栈

    mov cx,6    ;12字节长度循环6次
    mov bx,0    ;bx计算偏移量
    ;将num1和num2的所有字节都置为零
setZero:
    mov [num1+bx],0
    mov [num2+bx],0
    add bx,2    ;偏移量增加
    loop setZero

    ;打印输入提示信息
    mov ah,09h
    lea dx,choose 
    int 21h

    ;获取输入,并存到ax里
    call InputNum
    push ax     ;暂存ax

    mov ah,09h
    lea dx,enter;打印回车
    int 21h

    pop ax      ;取出ax
    cmp ax,0    ;判断是否为0
    je ProcWrongRange
    cmp ax,99 ;判断是否比100大
    ja ProcWrongRange


    call Fib    ;调用斐波那契数列迭代计算模块，结果存在num2里

    mov ah,09h
    lea dx,result   ;输出答案提示信息
    int 21h

    call LongNumPrint   ;调用超长整数输出模块

    mov ah,09h
    lea dx,enter;打印回车
    int 21h

    mov ah,09h
    lea dx,pressQ   ;提示退出信息
    int 21h

    mov ah,09h
    lea dx,enter;打印回车
    int 21h

    jmp start ;使用jmp形成死循环,程序正在的出口在数字输入模块里

ProcWrongRange:
    mov ah,09h
    lea dx,wrongRange   ;输出范围错误提示信息
    int 21h

    mov ah,09h
    lea dx,enter;打印回车
    int 21h

    jmp start   ;利用jmp形成死循环
;========
;===模块实现
;========
;=========程序出口======
ProcExit:
    mov ax, 4c00h
    int 21h
end start

无符号数字输入模块

柿子拣软的捏，所以我们先来实现最简单的输入模块

这个模块的功能需求有

  • 支持输入十进制数字串,并存储到ax输出
  • 支持判断是否输入Q，输入时跳转到退出程序
  • 可在输入非法字符（包括回车）时，停止输入，跳转到输出返回

初始化&现状保存

如同C语言函数的传值传参一样，我们也模拟函数的行为做传值传参。为此我们就要做现状保存。

现状保存的具体做法就是按一定顺序把需要保存的寄存器数据存入堆栈，函数返回前我们再逆序取出来。

至于如何传出获取到的数字，我们这里约定使用ax作为输出型参数输出寄存器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
;================数字键入模块============
InputNum:
    ;现状保存,除了ax要输出参数
    ;设计为传值传参，所以要保存bx~dx
    push bx  
    push cx  
    push dx  

    mov bx,0    ;要用bx所以提前置0,用于暂存结果
    mov cx,0    ;同理,但用于中间计算

    ;.... 中间代码....
    ;....函数功能完成,即将返回....
    ;开始恢复函数调用前的状态

InputNumEnd:
    mov ax,0
    mov al,bl   ;向ax存入结果
    pop dx; 恢复现场
    pop cx;
    pop bx;
    ret   ;函数返回

非法输入处理和数字存入

我们采用死循环的方式逐个字符即时读取，

为了防止Q被解析成非法字符，所以我们先判断输入是否为Q，若是，我们就跳转到程序退出。但是因为这里的代码长度问题，使用je可能会越界，所以我们使用了二级跳跃:je 配合 jmp far ptr使用

然后再判断到非法字符(非0~9数字字符)时模块跳出循环到模块结束部分InputNumEnd。

这里的判断非法字符我们要配合之前用过的cmp，这里用到的标志位是CF进位标志位和ZF零标志位,要用到的跳转函数是ja和jb

  • ja: Jump if Above,当op1 > op2时跳转
  • jb: Jump if Below，当op1 < op2时跳转

这样我们就能只取'0'和'9'中间的字符了,

至于数字存入，我们则是把暂存的结果（这里是bx）乘以10再加上ax里的尾数的数值

而如何实现x10操作呢？我们采用移位操作/乘以2的n次方 配合加法，即把bx*=10拆成bx = bx*2^3 + bx + bx

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
FarProcExit:
    jmp far ptr ProcExit    ;远距离跳转
    ret

InputLoop:
    mov ah,1h ;使用1号中断输入字符
    int 21h
    ;判断是否为字符Q,为Q则退出程序
    cmp al,'Q'
    je FarProcExit
    ;非法字符判断，包括回车时结束输入
    cmp al,'0' ;和字符'0'比较
    jb InputNumEnd  ;jb用于比小，当al < '0'小时跳转
    cmp al,'9'
    ja InputNumEnd  ;ja用于比大，当al > '0'时跳转

    sub al,'0' ;减去'0'获得真实数值   字符->数字
    ;实现bx*=10,即 bx = bx*2^3 + bx + bx
    mov cl,bl   ;备份bl的值
    shl bx,1    ;不能一次性移3位，会报错
    shl bx,1    ;
    shl bx,1    ;左移3位，相当于*8
    add bl,cl   ;
    add bl,cl   ;加两次
    add bl,al   ;把尾数al加上去

    jmp InputLoop ;重新循环

模块的完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
;================数字键入模块============
FarProcExit:
    jmp far ptr ProcExit    ;远距离跳转
    ret

InputNum:
    ;现状保存,除了ax要输出参数
    ;设计为传值传参，所以要保存bx~dx
    push bx  
    push cx  
    push dx  

    mov bx,0    ;要用bx所以提前置0,用于暂存结果
    mov cx,0    ;同理,但用于中间计算
InputLoop:
    mov ah,1h ;使用1号中断输入字符
    int 21h
    ;判断是否为字符Q,为Q则退出程序
    cmp al,'Q'
    je FarProcExit
    ;非法字符判断，包括回车时结束输入
    cmp al,'0' ;和字符'0'比较
    jb InputNumEnd  ;jb用于比小，当al < '0'小时跳转
    cmp al,'9'
    ja InputNumEnd  ;ja用于比大，当al > '0'时跳转

    sub al,'0' ;减去'0'获得真实数值   字符->数字
    ;实现bx*=10,即 bx = bx*2^3 + bx + bx
    mov cl,bl   ;备份bl的值
    shl bx,1    ;不能一次性移3位，会报错
    shl bx,1    ;
    shl bx,1    ;左移3位，相当于*8
    add bl,cl   ;
    add bl,cl   ;加两次
    add bl,al   ;把尾数al加上去

    jmp InputLoop ;重新循环

InputNumEnd:
    mov ax,0
    mov al,bl   ;向ax存入结果
    pop dx; 恢复现场
    pop cx;
    pop bx;
    ret    ;函数返回

斐波那契数输出模块/超长整型输出模块

使用万进制的内存存储

大于双字（无法加载到内存器中）的二进制数转十进制太麻烦太难了，所以我们退而求其次，将其变成万进制转十进制，这样的转换就简单多了。因此我们对内存的分块的视图如下:

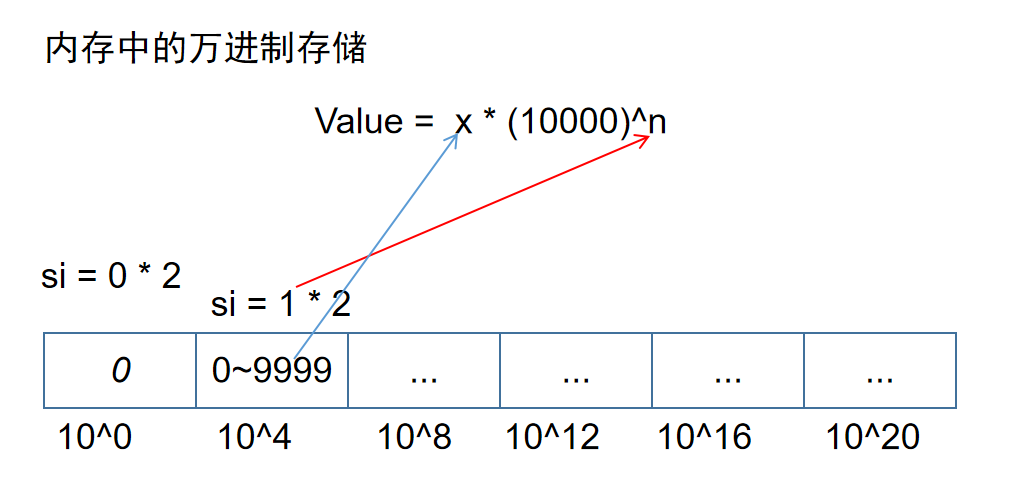
显然我们引入了一个前提:一个字内的值不会超过9999，这一前提的实现我们交给迭代求值模块来实现

万进制的好处

使用万进制存储的最大的好处就是映射关系简单，我们可以简单地按字处理数字字符的转换,因为它的映射关系就是按字分块的

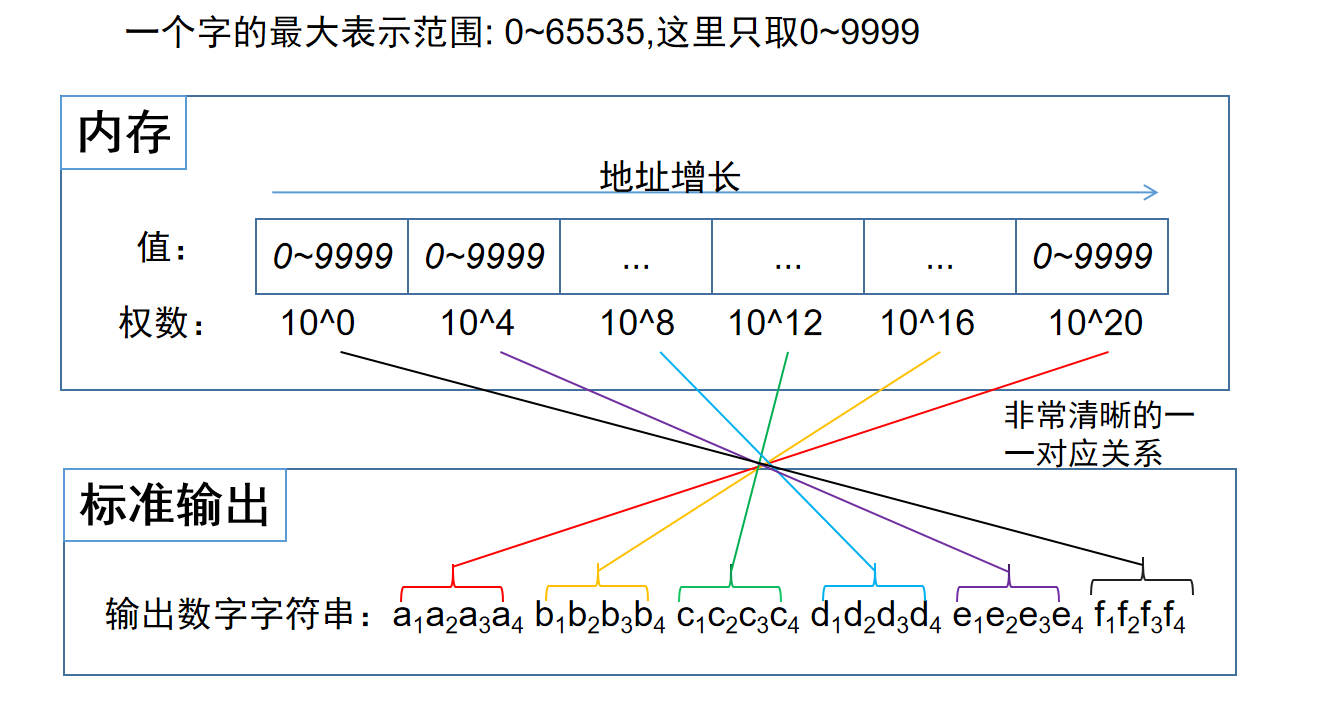
代码实现

基于万进制存储的思想，我们借助栈来产生数字字符串

当然，我们还有前导零的删除和中间0的输出要处理

删除前导零

思路上很简单，我们在产生数字字符时，适时地判断整个连续内存是否为0，若为0，显然此时产生的是前导零，我们可以直接跳转到输出子模块，这样就可以方便地删除前导零了。不过显然整个连续内存的判0较为复杂，所以我们还要封装一个判0模块来使用，同时也能防止一个模块内代码量过大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
;========判空模块==========
isLongZero:
    push cx
    push si
    mov cx,6  ;循环6次
    mov si,0
isLongZeroLoop:
    mov ax,[num2+si]
    cmp ax,0
    jnz ZeroFalse
    add si,2
    loop isLongZeroLoop

ZeorTrue:
    pop si
    pop cx
    mov ax,1
    ret
ZeroFalse:
    pop si
    pop cx
    mov ax,0
    ret

输出中间0

当高位内存不为0时，我们要保证输出够中间0，所以我们使用四次循环打印配合cmp分流的方式，保证每一段内存，在高位不为0时，输出足够的中间0

输出一般数字字符

这里我们依然采用除以10求余法来获取每一位数字，然后加上'0'来转换为数字字符

至于顺序问题，我们会先求出来最低位的数字字符，但是我们要最后打印最低位数字字符，所以我们使用栈来暂存数字字符，最后出栈时就能很好地逆序输出。显然对同一个字内的值是这样，对于字与字之间，我们要先求低位字的数字字符再求高位的，这样能达到整体数字的顺序一致性

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
;========Fib数字输出模块=====
;要先打印高位,答案在num2
LongNumPrintZero:
    mov dx,'0'    ;打印0
    mov ah,02h;打印字符指令
    int 21h     ;开启中断
    ret

LongNumPrint:
    mov ax,0
    mov [numlen],ax  ;numlen储存输出长度
    call isLongZero ;判0
    cmp ax,1    ;为0时直接打印0
    jz LongNumPrintZero

    mov si,0  ;存储偏移量
    mov cx,6 ;6个字
LongParseLoop:
    call isLongZero
    cmp ax,1  
    jz LongNumPrintOutput   ;为0则停止分析,开始打印输出

    mov [tmpcx1],cx ;暂存cx
    mov cx,4   ;每个单元最多存储9999,所以要固定打印3位数字
FourLoop:
    call isLongZero
    cmp ax,1    ;判断是否为0
    jnz FourLoopStart  ;不为零则进入循环
    ;循环出口
    ;为0则不管外层cx，直接前去打印
    jmp LongNumPrintOutput
FourLoopStart:
    add [numlen],1

    mov ax,[num2+si]
    cmp ax,0 
    jz FourLoopZero    ;分流

    mov dx,0
    mov bx,10
    div bx
    mov [num2+si],ax    ;写回内存
    add dx,'0'  ;转换为字符
    jmp FourLoopAdd

FourLoopZero:
    mov dx,'0'
FourLoopAdd:
    push dx
    loop FourLoop

    mov cx,[tmpcx1]
    add si,2 ;增加偏移量
    loop LongParseLoop

LongNumPrintOutput:
    mov cx,[numlen] ;取出数字长度
LongNumPrintOutputLoop:
    pop dx    ;出栈
    mov ah,02h;打印字符指令
    int 21h     ;开启中断
    loop LongNumPrintOutputLoop

    ret


;========判空模块==========
isLongZero:
    push cx
    push si
    mov cx,6  ;循环6次
    mov si,0
isLongZeroLoop:
    mov ax,[num2+si]
    cmp ax,0
    jnz ZeroFalse
    add si,2
    loop isLongZeroLoop

ZeorTrue:
    pop si
    pop cx
    mov ax,1
    ret
ZeroFalse:
    pop si
    pop cx
    mov ax,0
    ret

斐波那契数列迭代模块

对于这一模块，我们采用ax输入参数，num2长内存输出结果。

以及我们要使用多位字节来储存大数字来应对溢出的风险。

迭代法求斐波那契数列

首先我们学习一下如何用最少的变量来迭代求斐波那契数列

  1. ax存储Fib(n-2)
  2. bx存储Fib(n-1),显然初始化时，bx是ax的后一位
  3. add ax,bx 求得Fib(n) = Fib(n-1) + Fib(n-2)，此时ax是bx的后一位
  4. 交换ax和bx的值,此时bx重新成为ax的后一位,并且ax和bx都在斐波那契数列中向后走了一位
  5. 回到第一步继续循环迭代

超长整数迭代斐波那契数列

这里我们使用了多字的num1和num2分别存储Fib(n-2)和Fib(n-1),所以我们要实现多字整型的加法。这里我们使用循环来从低位往高位相加,当然，我们顺便也可以在加完后就交换低位的内存。

但是在加的时候，我们同时要考虑进位，，因为相加结果存在了ax，所以要及时判断ax的值是否超过了9999，若是，则减去10000，同时让高位+1。那么怎么加呢？我们可以用别的寄存器来临时存储，但其实我们可以直接加到内存中，在接下来的更高地址的字的运算里用到。那么问题来了，num1和num2加给谁呢？考虑到,num2表示Fib(n-1)，在本次运算后要交换给num1，其正确性不能被低位的进位破坏，而num1原本的值本来就会在运算后被覆盖，所以把进位加给num1的就非常合适

代码实现

具体输出时还要考虑最基本的情况:Fib(1) = Fib(2) = 1，所以我们在输入时再加一个判断，单独输出这俩结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
;===========斐波那契数列迭代模块========规定用num2输出
Fib:
    cmp ax,3 ;ax <3 ，或者说 ax <= 2时
    jb FibBaseRet

    mov cx,ax
    sub cx,1    ;循环n-1次
    mov dx,0    ;储存进位
    mov ax,0
    mov bx,1
    mov [num1],ax   ;存入初始值
    mov [num2],bx
FibLoop:
    push cx ;暂存最外部的循环
    ;内层循环初始化
    mov si,0    ;储存偏移量
    mov cx,6    ;开始逐段相加和交换
FibInnerLoop:
    mov ax,[num1+si];//从低位到高位取出一段数据
    mov bx,[num2+si];
    add ax,bx   ;计算相加

    cmp ax,9999
    ja  FibCB
FibNoneCB:
    jmp FIBExchange
FibCB:
    sub ax,10000 ;减去1000
    add [num1+si+2],1   ;加上进位，因为num2+si+2要用于下次的赋值，所以不能加在上面
FIBExchange:
    ;交换ax,bx
    push ax
    push bx
    pop ax
    pop bx

    mov [num1+si],ax    ;将数据写回内存
    mov [num2+si],bx 
    add si,2
    loop FibInnerLoop
    pop cx ;走到这完成了一次数字相加和交换,所以要回到外层循环
    loop FibLoop    

    ;输出参数在num2
    ret 

FibBaseRet:
    ;Fib(1) = Fib(2) = 1
    mov ax,1    ;ax输出参数
    mov [num2],ax;
    ret

整个项目的代码

在完成了数个模块后，我们终于可以把它们都拼接在一块了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
assume cs:codesg,ds:datasg,ss:stacksg

;初始化数据段，并填入数字
datasg segment
    choose db 'Please choose a num from 1 to 100 : ','$'
    result db 'The result is : ','$'
    pressQ db 'Presss Q to exit','$'
    wrongRange db 'wrong range, try again'
    enter db 13, 10,'$'
    num1 dw 6 dup(0)
    num2 dw 6 dup(0)

    numlen dw 0 ;储存输出长度

    tmpcx1 dw 0

datasg ends  

;初始化栈段，置空
stacksg segment
    db 25565 dup(0)
stacksg ends  



codesg segment
start:  
    mov ax,datasg 
    mov ds,ax;
    mov ax,stacksg;
    mov ss,ax;
    mov sp,25565;初始化栈

    mov cx,6    ;12字节长度循环6次
    mov bx,0    ;bx计算偏移量
    ;将num1和num2的所有字节都置为零
setZero:
    mov [num1+bx],0
    mov [num2+bx],0
    add bx,2    ;偏移量增加
    loop setZero

    ;打印输入提示信息
    mov ah,09h
    lea dx,choose 
    int 21h

    ;获取输入,并存到ax里
    call InputNum
    push ax     ;暂存ax

    mov ah,09h
    lea dx,enter;打印回车
    int 21h

    pop ax      ;取出ax
    cmp ax,0    ;判断是否为0
    je ProcWrongRange
    cmp ax,99 ;判断是否比100大
    ja ProcWrongRange


    call Fib    ;调用斐波那契数列迭代计算模块，结果存在num2里

    mov ah,09h
    lea dx,result   ;输出答案提示信息
    int 21h

    call LongNumPrint   ;调用超长整数输出模块

    mov ah,09h
    lea dx,enter;打印回车
    int 21h

    mov ah,09h
    lea dx,pressQ   ;提示退出信息
    int 21h

    mov ah,09h
    lea dx,enter;打印回车
    int 21h

    jmp start ;使用jmp形成死循环,程序正在的出口在数字输入模块里

ProcWrongRange:
    mov ah,09h
    lea dx,wrongRange   ;输出范围错误提示信息
    int 21h

    mov ah,09h
    lea dx,enter;打印回车
    int 21h

    jmp start   ;利用jmp形成死循环
;===========斐波那契数列迭代模块========规定用num2输出
Fib:
    cmp ax,3 ;ax <3 ，或者说 ax <= 2时
    jb FibBaseRet

    mov cx,ax
    sub cx,1    ;循环n-1次
    mov dx,0    ;储存进位
    mov ax,0
    mov bx,1
    mov [num1],ax   ;存入初始值
    mov [num2],bx
FibLoop:
    push cx ;暂存最外部的循环
    ;内层循环初始化
    mov si,0    ;储存偏移量
    mov cx,6    ;开始逐段相加和交换
FibInnerLoop:
    mov ax,[num1+si];//从低位到高位取出一段数据
    mov bx,[num2+si];
    add ax,bx   ;计算相加

    cmp ax,9999
    ja  FibCB
FibNoneCB:
    jmp FIBExchange
FibCB:
    sub ax,10000 ;减去1000
    add [num1+si+2],1   ;加上进位，因为num2+si+2要用于下次的赋值，所以不能加在上面
FIBExchange:
    ;交换ax,bx
    push ax
    push bx
    pop ax
    pop bx

    mov [num1+si],ax    ;将数据写回内存
    mov [num2+si],bx 
    add si,2
    loop FibInnerLoop
    pop cx ;走到这完成了一次数字相加和交换,所以要回到外层循环
    loop FibLoop    

    ;输出参数在num2
    ret 

FibBaseRet:
    ;Fib(1) = Fib(2) = 1
    mov ax,1    ;ax输出参数
    mov [num2],ax;
    ret 
    
;================数字键入模块============
FarProcExit:
    jmp far ptr ProcExit    ;远距离跳转
    ret

InputNum:
    ;现状保存,除了ax要输出参数
    ;设计为传值传参，所以要保存bx~dx
    push bx  
    push cx  
    push dx  

    mov bx,0    ;要用bx所以提前置0,用于暂存结果
    mov cx,0    ;同理,但用于中间计算
InputLoop:
    mov ah,1h ;使用1号中断输入字符
    int 21h
    ;判断是否为字符Q,为Q则退出程序
    cmp al,'Q'
    je FarProcExit
    ;非法字符判断，包括回车时结束输入
    cmp al,'0' ;和字符'0'比较
    jb InputNumEnd  ;jb用于比小，当al < '0'小时跳转
    cmp al,'9'
    ja InputNumEnd  ;ja用于比大，当al > '0'时跳转

    sub al,'0' ;减去'0'获得真实数值   字符->数字
    ;实现bx*=10,即 bx = bx*2^3 + bx + bx
    mov cl,bl   ;备份bl的值
    shl bx,1    ;不能一次性移3位，会报错
    shl bx,1    ;
    shl bx,1    ;左移3位，相当于*8
    add bl,cl   ;
    add bl,cl   ;加两次
    add bl,al   ;把尾数al加上去

    jmp InputLoop ;重新循环

InputNumEnd:
    mov ax,0
    mov al,bl   ;向ax存入结果
    pop dx; 恢复现场
    pop cx;
    pop bx;
    ret    ;函数返回


;========Fib数字输出模块=====
;要先打印高位,答案在num2
LongNumPrintZero:
    mov dx,'0'    ;打印0
    mov ah,02h;打印字符指令
    int 21h     ;开启中断
    ret

LongNumPrint:
    mov ax,0
    mov [numlen],ax  ;numlen储存输出长度
    call isLongZero ;判0
    cmp ax,1    ;为0时直接打印0
    jz LongNumPrintZero

    mov si,0  ;存储偏移量
    mov cx,6 ;6个字
LongParseLoop:
    call isLongZero
    cmp ax,1  
    jz LongNumPrintOutput   ;为0则停止分析,开始打印输出

    mov [tmpcx1],cx ;暂存cx
    mov cx,4   ;每个单元最多存储9999,所以要固定打印3位数字
FourLoop:
    call isLongZero
    cmp ax,1    ;判断是否为0
    jnz FourLoopStart  ;不为零则进入循环
    ;循环出口
    ;为0则不管外层cx，直接前去打印
    jmp LongNumPrintOutput
FourLoopStart:
    add [numlen],1

    mov ax,[num2+si]
    cmp ax,0 
    jz FourLoopZero    ;分流

    mov dx,0
    mov bx,10
    div bx
    mov [num2+si],ax    ;写回内存
    add dx,'0'  ;转换为字符
    jmp FourLoopAdd

FourLoopZero:
    mov dx,'0'
FourLoopAdd:
    push dx
    loop FourLoop

    mov cx,[tmpcx1]
    add si,2 ;增加偏移量
    loop LongParseLoop

LongNumPrintOutput:
    mov cx,[numlen] ;取出数字长度
LongNumPrintOutputLoop:
    pop dx    ;出栈
    mov ah,02h;打印字符指令
    int 21h     ;开启中断
    loop LongNumPrintOutputLoop

    ret


;========判空模块==========
isLongZero:
    push cx
    push si
    mov cx,6  ;循环6次
    mov si,0
isLongZeroLoop:
    mov ax,[num2+si]
    cmp ax,0
    jnz ZeroFalse
    add si,2
    loop isLongZeroLoop

ZeorTrue:
    pop si
    pop cx
    mov ax,1
    ret
ZeroFalse:
    pop si
    pop cx
    mov ax,0
    ret
;=========程序出口======
ProcExit:
    mov ax, 4c00h
    int 21h
codesg ends
end start