整型家族

在使用C语言写程序时，会储存各种长度的整型,而在整型家族中，长度的比较如下

char < short <= int <= long <long long

整型是如何储存在内存中的

以char为例
char

char的长度为1个字节，8个比特位,其中最高位是符号位,0表示正数，1表示负数，剩下的位数用于储存变量的绝对值

而当使用无符号整型(带前缀unsigned)时，只需把符号位也用于存值即可

能够储存的最大正整数

int长度为4字节,能够储存的最大值为2的31次方-1,即2,147,483,647

unsigned int能够储存的最大值为4294967295

unsigned long long长度为8字节,能够储存的最大值为2的64次方-1,即18,446,744,073,709,551,615

限制

虽然unsigned long long已经很大了，但当遇到指数,阶乘之类的运算时仍然可能存不下!(光21!就比unsigned long long长了)

思路

过大的整数，可能出现在程序的过程中，也可能出现在输出中，对于过程，可以尝试改变实现思路，让过程中不出现过大的整数；对于输出，可以尝试改变输出的类型，采用输出字符或字符串

以下皆为例题

1.求n!的结尾有多少个0

最直白的思路就是把n!算出来，然后用%10再/=10的方法统计末尾的0,想法很简单，“实现”起来也不难，但不幸的是，21!就已经储存不了了，所以不能暴力求解

所以要改变思路，先从末尾0是怎么来的下手。末尾的n个0来自因式分解后10的n次方，而采用质因数分解的方法，可以发现0来自分解后2的n次方和5的n次方,而一个数分解后2的n次方必定比5的n次方 多，所以只需统计5的n次方。注意：就别再倒回去，想着先算出阶乘再求5的n次方了。

这里采用逐步计数的方法：结果中的5的n次方来自各个因数中5的N次方的累乘,所以只需要历遍每个因数，并统计其中因数5的次数。这样过程中就不会有过大的数字了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//代码实现
int count_num0(int n)
{
    int count = 0;
    for(int i = 1;i<=n;i++)
    {
        int copy = i//防止改变循环变量
        while(copy%5 == 0)//统计因数5的出现次数
        {
            if(copy%5 == 0)
            {
                count++;
            }
            copy/=5;
        }
    }

    return count;
}

快速输出1+2+……+10^n

如下图：当我们试图算一算答案时，发现n到了10时就已经算不出答案了

计算结果

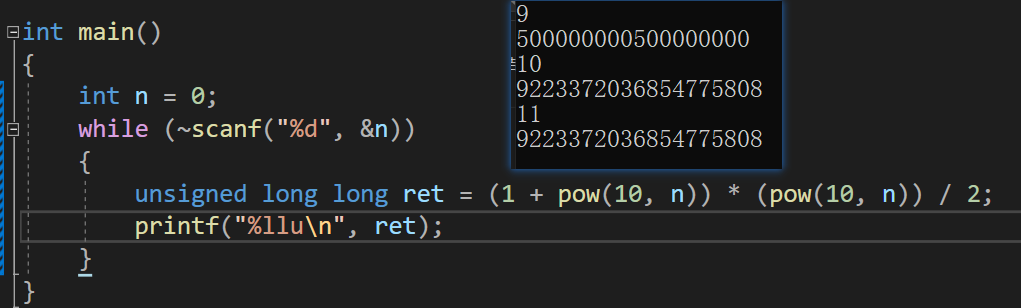
所以要改变输出答案答案的方式,观察一下n在1~9时的输出

输出

这时我们发现答案颇有规律：每个输出都是两段先一个5，然后n-1个0！

这样我们只需从最高位往最低位逐位打印即可,代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void printChar(int n)//版本一，逐位打印字符(串)
{
    printf("5");
    for(int i =0;i<n-1;i++)
    {
        printf("0");
    }
    //再重复一段
    printf("5");
    for(int i =0;i<n-1;i++)
    {
        printf("0");
    }
    printf("\n");
}

void printNum(int n)//版本二，逐位打印整型
{
    printf("%d",5);
    for(int i =0;i<n-1;i++)
    {
        printf("%d",0);
    }
    //再重复一段
    printf("%d",5);
    for(int i =0;i<n-1;i++)
    {
        printf("%d",0);
    }
    printf("\n");
}