背景知识

  • 知道什么是大堆/小堆
  • 掌握如何将数组与完全二叉树的映射关系
  • 掌握向上调整法和向下调整法

大堆/小堆

大堆的特性:每一个节点的值都比左右孩子都大,根的值是整个大堆中最大的
小堆的特性:每一个节点的值都比左右孩子都小,根的值是整个大堆中最小的

后面以大堆为例

数组映射成完全二叉树

任何一个数组可以看成一个完全二叉树,下标0为二叉树的根

而非常方便的是，已知一个节点的下标，可以利用数学关系求出根或孩子的下标

下标关系如下（变量均为下标）

  • parent = (child-1)/2
  • left_child = parent*2+1
  • right_child = parent*2+2

建堆方法

向上调整法

在已有一个大堆的前提下,把一个新的数据插入到堆的最后一个节点(此时破坏大堆的结构),再一路向上调整,可以重新建堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template<class T>
void adjust_up(vector<T>& arr, int child)
{
	int parent = (child - 1) / 2;
	while (parent != child)//parent == child == 0时
	{
		if (arr[parent] < arr[child])//不满足大堆
		{
			swap(arr[parent], arr[child]);//交换
			child = parent;//继续向上调整,迭代child和parent
			parent = (child - 1) / 2;
		}
		else//完成建堆，退出循环
		{
			break;
		}
	}
}

向下调整法

在已有一个大堆的前提下,把根的值改变(此时破坏大堆的结构),再一路向下调整，可以重新建堆

上一句也可以等价于,左子树和右子树都是大堆的前提下，将根一路向下调整，可以重新建堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
template<class T>
void adjust_down(vector<T>& arr,int sz , int parent)
{
	int child = parent * 2 + 1;
	if (child + 1 < sz && arr[child + 1] > arr[child]) child++;//取较大的孩子

	while (child < sz)
	{
		if (arr[parent] < arr[child])
		{
			swap(arr[parent], arr[child]);
			parent = child;
			int child = parent * 2 + 1;
			if (child >= sz) break;
			if (child + 1 < sz && arr[child + 1] > arr[child]) child++;
		}
		else
		{
			break;
		}
	}
}

主要思路

建堆

用向上调整法和向下调整法都能建堆,不过向上调整法建堆思路更简单，也更容易代码实现，只需要把第一个元素当成现成的大堆，然后逐个插入并向上调整。也就是说只需要写一个循环

1
2
3
4
5
//向上调整法建堆
for (int i = 1; i < sz; i++)
{
    adjust_up(arr, i);//逐个插入并向上调整建堆
}

排序

此时的排序有个特点，那就是我们要倒着排

尽管此时数组的第一个元素为最大值,似乎只需要把它放在那，整一个降序排列，再把剩下的元素建个堆，确定第二大的数…但是，此时有个很大的问题，当把剩下的元素看作堆时，会发现前面建堆留下来的关系全被打乱了(原本父子关系,兄弟关系乱套了),也就是说要完全重新建堆,极大地浪费了第一次建堆所建立的关系

所以我们要尽可能保留原来的堆,既然把下标0处的节点除外会极大地影响堆的关系，那就改成把最后一个叶子节点除外,这样对原来的堆几乎没有改变。

但建堆选出的最大的的值在根处,所以把根和最后一个叶子节点交换，交换后,此时待排序的数中的最大值以完成排序（即倒着排）,把最后一个叶子节点从堆中除外,再从根开始一路向下调整即可重新建堆,如此循环

1
2
3
4
5
for (int i = sz-1; i >= 1; i--)//利用i的减小将已排序的元素逐个除外
{
	swap(arr[0], arr[i]);//选出最大的元素放在末尾
	adjust_down(arr,i,0);//向下调整建堆,待排序的（待建堆的）数的个数为i,逐个减小
}

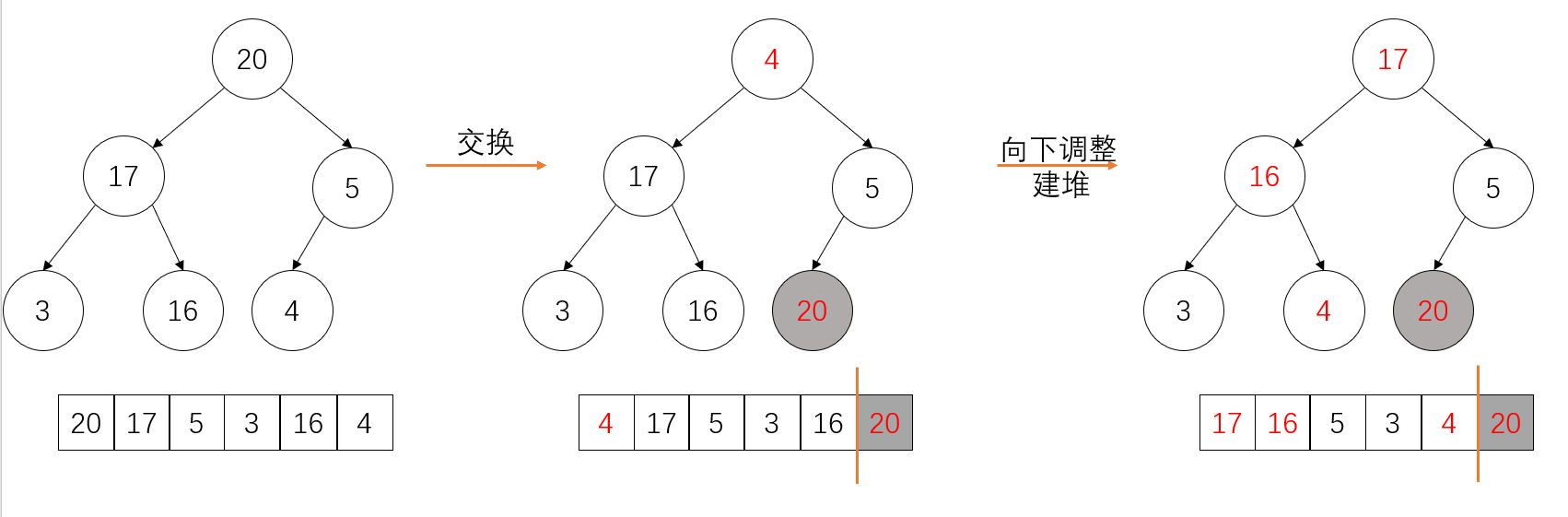
正因为实际上排序时是倒着排的,所以当我们要排序时：

  • 升序->大堆
  • 降序->小堆

全部代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include <vector>
using namespace std;

template<class T>
void adjust_up(vector<T>& arr, int child)
{
	int parent = (child - 1) / 2;
	while (parent != child)//parent == child == 0时
	{
		if (arr[parent] < arr[child])//不满足大堆
		{
			swap(arr[parent], arr[child]);//交换
			child = parent;//继续向上调整,迭代child和parent
			parent = (child - 1) / 2;
		}
		else//完成建堆，退出循环
		{
			break;
		}
	}
}

template<class T>
void adjust_down(vector<T>& arr,int sz , int parent)
{
	int child = parent * 2 + 1;
	if (child + 1 < sz && arr[child + 1] > arr[child]) child++;//取较大的孩子

	while (child < sz)
	{
		if (arr[parent] < arr[child])
		{
			swap(arr[parent], arr[child]);
			parent = child;
			int child = parent * 2 + 1;
			if (child >= sz) break;
			if (child + 1 < sz && arr[child + 1] > arr[child]) child++;
		}
		else
		{
			break;
		}
	}
}

template <class T>
void heap_sort(vector<T>& arr)
{
	int sz = arr.size();

	//建堆
	for (int i = 1; i < sz; i++)
	{
		adjust_up(arr, i);//逐个插入并向上调整建堆
	}

	for (int i = sz-1; i >= 1; i--)
	{
		swap(arr[0], arr[i]);//选出最大的元素放在末尾
		adjust_down(arr,i,0);//向下调整建堆
	}
}